ο τοίχος των κλασμάτων 2

Ποιο είναι μεγαλύτερο το ένα τρίτο ή τα δύο όγδοα; Πόση είναι η διαφορά τους; Αξιοποιήστε την εικόνα του τοίχου των κλασμάτων για να βεβαιωθείτε ότι απαντήσατε σωστά.
Ποιο είναι μικρότερο τα πέντε έκτα ή  τρία τέταρτα; Πόση είναι η διαφορά τους;
Ποια είναι διαφορά ανάμεσα στα πέντε έκτα και το ένα τρίτο;
Ποια είναι τα τρία τέταρτα του δύο τρίτα; Μπορείς να εξηγήσεις πως το βρήκες;

Σοκολάτα

Στη δραστηριότητα αυτή ασχολούμαστε με σοκολάτες. Φανταστείτε ότι όσοι συμμετέχουν σ' αυτή θέλουν να πάρουν όσο το δυνατόν περισσότερη. 

Σε μια αίθουσα του σχολείου έχουμε τρία τραπέζια και άφθονο χώρο γύρω τους για να βάλουμε όσες σοκολάτες θέλουμε. Στο πρώτο τραπέζι έχουμε μια πλάκα σοκολάτας, στο δεύτερο τραπέζι δύο μπάρες και στο τρίτο 3.   

Έξω από την αίθουσα υπάρχει μια μεγάλη ουρά μαθητών που περιμένουν να πάρουν τις σοκολάτες. Ο κανόνας λέει ότι κάθε παιδί μπαίνει στην αίθουσα, μονάχα αφού ο μπροστινός του έχει ήδη κάτσει. Μετά διαλέγει τραπέζι και από την στιγμή που θα κάτσει δικαιούται το μερίδιο που του αναλογεί από το τραπέζι. Έτσι όποτε κάποιος μπαίνει στην αίθουσα πρέπει να αναλογιστεί: "Αν η σοκολάτα του τραπεζιού που θα διαλέξω μοιραστεί δίκαια, σε ποιο τραπέζι με συμφέρει να κάτσω;" Κανείς δεν ξέρει σε ποιο σημείο θα απαγορευτεί η είσοδος κι άλλων μαθητών.

Ωστόσο, η πράξη της μοιρασιάς δεν αρχίζει μέχρις ότου κάτσουν όλα τα παιδιά.  

Είναι μάλλον εύκολο να διαλέξει κανείς τραπέζι αν είναι στην αρχή. Όσο όμως προχωρά η διαδικασία γίνεται όλο και δυσκολότερο.  

Ας πούμε ότι έχουν ήδη μπει 8 παιδιά. Τώρα είναι η σειρά σας. Μπαίνετε στο δωμάτιο και βλέπετε  

• 2 παιδιά στο πρώτο τραπέζι 
• 
  
• 3 παιδιά στο δεύτερο τραπέζι
  
• 3 παιδιά στο τρίτο τραπέζι
  

Πώς θα διαλέξετε τραπέζι;
Εγώ στη θέση σας θα σκεφτόμουν 

"αν πάω στο πρώτο τραπέζι θα γίνουμε τρεις, θα πάρω δηλαδή το 1/3,
αν πάω στο δεύτερο θα γίνουμε 4, θα πάρω δηλαδή τα 2/4,
αν πάω στο τρίτο τραπέζι θα γίνουμε 4, θα πάρω δηλαδή τα 3/4. Τα 3/4 είναι η καλύτερη (μεγαλύτερη) από τις επιλογές μου, άρα θα πάω στο τρίτο τραπέζι."

Συνεχίστε και βρείτε τι μέρος της σοκολάτας παίρνει το κάθε παιδί, καθώς συνεχίζεται η μοιρασιά. Σταματήστε όταν φτάσετε στο 30ο παιδί. Καταγράψτε τις ιδέες σας με τη σειρά που προκύπτουν.

Στη συνέχεια συζητήστε με συμμαθητές σας και συγκρίνετε την πορεία που σκεφτήκατε με τη δική τους. Διαλέξτε ποια διαδρομή ήταν η καλύτερη κατά τη γνώμη σας και εξηγήστε το γιατί.

ο τοίχος των κλασμάτων

Χρησιμοποιώντας την παραπάνω εικόνα, βρείτε όλους τους δυνατούς τρόπους για να γράψατε με κλάσμα το μισό.1

Με τη βοήθεια της εικόνας, μπορείτε να βρείτε ισοδύναμα του 13 ;  πόσα;

Χρησιμοποιώντας και πάλι την εικόνα του τοίχου των κλασμάτων, γράψτε με διαφορετικούς τρόπους τα 34;

Μήπως μπορείτε να βρείτε κάποιον κανόνα για να δουλεύετε με τα ισοδύναμα κλάσματα;

Κλάσματα μήκους

Στο παρακάτω σχέδιο μπορείτε να δείτε 7 μπάρες διαφορετικού χρώματος. Κάθε μία φτιάχνεται από διαφορετικό πλήθος τετράγωνων, το οποίο είναι γραμμένο στο τέλος της. 

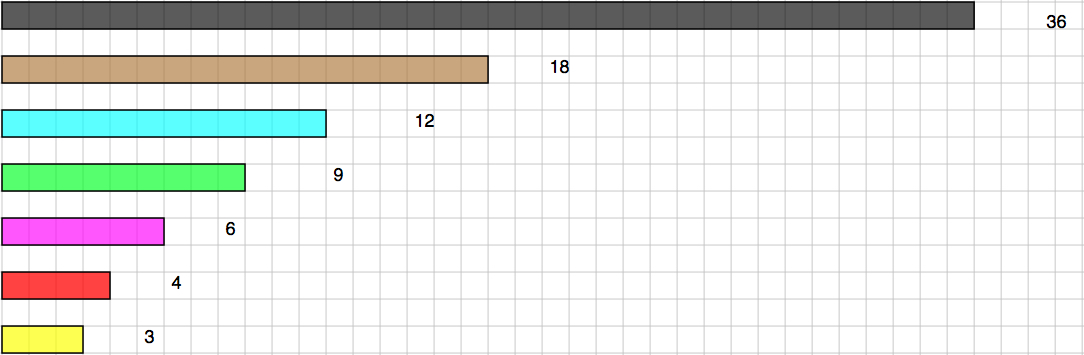
Για να ξεκινήσετε υπολογίστε τη μαύρη μπάρα ως 1, άρα η καφέ είναι το

12 τη, η μπλε το 13, κλπ.

Χρησιμοποιώντας διαφορετικούς συνδυασμούς, προσπαθήστε να φτάσετε στο μήκος της μαύρης μπάρας, δηλαδή στο 36.

Στη συνέχεια γράψτε τη λύση σας με δύο τρόπους. 

Για παράδειγμα αν βάλετε την καφέ μπάρα μαζί με τη γαλάζια και την ροζ θα τα έχετε καταφέρει και πρέπει να γράψετε:

α. 

18 + 12 + 6 = 36

και β.

12+13+16=1

- - - - - - - - - - - - - - - - - -

Συνέχεια 1

Διαλέξτε 4 μπάρες (εκτός από τη μαύρη) και συγκρίνετε το άθροισμα τους με τη μαύρη μπάρα.  

Ακολουθούν δύο παραδείγματα:  

1.

Αθροίζοντας το κίτρινο (3), το ροζ (6), το γαλάζιο (12) και το καφέ (18), 

φτάνουμε 39, δηλαδή στο 1 ολόκληρο και ένα δωδέκατο.

2.  Χρησιμοποιώντας 2 γαλάζια (2Χ12) και δύο πράσινα (2Χ9) φτάνουμε στο 42, δηλαδή στο 1 ολόκληρο και ένα έκτο.

 1

112

16

- - - - - - - - - - - - - - - - - - 

Συνέχεια 2

Τώρα η γαλάζια μπάρα θα είναι το 1. Χρησιμοποιήστε τις τετράδες που έχετε ήδη φτιάξει, και συγκρίνετε τις με τη γαλάζια, αντί για τη μαύρη μπάρα.

Στο πρώτο από τα παραδείγματα μας  (κίτρινο + ροζ + γαλάζιο + καφέ) η σύγκριση θα μας έβγαζε  τρεις ολόκληρες γαλάζιες μπάρες και ένα τέταρτο της. 

Στο δεύτερο παράδειγμα ( γαλάζια + γαλάζια + πράσινη + πράσινη) η σύγκριση θα μας έβγαζε 3 γαλάζιες και μισή ακόμη.

Τώρα κάνετε τις δικές σας συγκρίσεις.

- - - - - - - - - - - - - - - - - -

Πως θα σχολιάζατε τα αποτελέσματα των συγκρίσεων πρώτα με τη μαύρη μπάρα και μετά με την γαλάζια; 

πηγή: https://nrich.maths.org/12935 

μοιράζοντας πίτσες

Όλη η παρέα μου τρελαίνεται για πίτσα.

Καλό είναι αυτό, γιατί συμφωνούμε όταν διαλέγουμε να φάμε κάτι μαζί. Το πρόβλημα είναι ότι συχνά τσακωνόμαστε για τη μοιρασιά. Θέλουμε δίκαιες και ίσες μοιρασιές. Μπορείς να βοηθήσεις;

Αν έχω μια πίτσα και θέλω να τη μοιραστώ με ένα φίλο, τι μέρος της πίτσας θα πάρει ο καθένας;
Τι μέρος θα πάρει ο καθένας αν θέλω να την μοιραστώ με δύο φίλους;

Μερικές φορές πρέπει να μοιράσουμε κάποιο μέρος της πίτσας που έχει περισσέψει από την προηγούμενη μέρα.

Αν έχω 1/2 της πίτσας και θέλω να την μοιραστώ με ένα φίλο μου, τι μέρος της ολόκληρης (ακέραιας) πίτσας θα πάρει ο καθένας;)

Αν έχει περισσέψει το 1/3 της πίτσας και θέλω πάλι να τη μοιραστώ με ένα φίλο μου, τι μέρος της ολόκληρης (ακέραιας) πίτσας θα πάρει ο καθένας; 

Κι αν ήμασταν τρεις που θα μοιράζονταν το 1/4 της πίτσας, τι θα γινόταν; Πόσο θα έπαιρνε ο καθένας; 

Μπορείς να εξηγήσεις πως σκέφτηκες για να απαντήσεις στις ερωτήσεις αυτές. Γράψε τη σκέψη σου.

Αν ο καθένας από την παρέα θέλει να πάρει 1/2  της πίτσας, πόσες πίτσες χρειαζόμαστε για 2 άτομα; πόσοι θα ικανοποιηθούν με δύο πίτσες;

Μπορείς να σκεφτείς έναν τρόπο για να γράψεις την σκέψη σου με πράξεις,

Μερικές φορές μπορεί να πεινάμε λίγο περισσότερο κι ο καθένας μας να θέλει 2/3 της πίτσας.
Πόσες πίτσες χρειαζόμαστε για 3 άτομα;
Πόσες για 4; Θα περισσέψει τίποτα;
Μπορείς να γράψεις τις σκέψεις σου με πράξεις;

Οι βόλοι του Βασίλη

Ο Βασίλης είχε βγει βόλτα με  το φίλο του το Δημήτρης. Ο Βασίλης είχε μαζί του ένα σακούλι με βόλους.  

Δυστυχώς για τον Βασίλη, ο πάτος του σάκου άνοιξε και οι βόλοι σκορπίστηκαν.  

Το ένα τρίτο (13) των βόλων κατρακύλησε πολύ γρήγορα στην κατηφόρα, χωρίς ο Βασίλης να προλάβει να μαζέψει κάποιον από αυτούς. Το ένα έκτο  (16) των βόλων έπεσε στον υπόνομο του δρόμου κι εξαφανίστηκε. 

Ο Βασίλης κι ο Δημήτρης μάζεψαν όσους μπορούσαν, αλλά τους μισούς από τους βόλους που είχαν απομείνει τους μάζεψαν κάτι πιτσιρίκια που εξαφανίστηκαν αστραπιαία.  

Ο Βασίλης μέτρησε τους βόλους που συγκέντρωσε με την βοήθεια του Δημήτρη. 

Στη συνέχεια, για να ευχαριστήσει έμπρακτα τον φίλο του για την βοήθεια του, τού χάρισε το ένα τρίτο  (13) από αυτούς.  Έβαλε τους υπόλοιπους 14 στην τσέπη και συνέχισε στενοχωρημένος, αλλά όχι απελπισμένος, την βόλτα του.

Πόσους βόλους είχε αρχικά ο Βασίλης;  

Τι κλάσμα του συνόλου των βόλων που είχε αρχικά έχασε ή έδωσε; 

πηγή: https://nrich.maths.org/2421

Λέλες και Μουμούς

Στον πλανήτη Βουβούς ζουν δύο ειδών πλάσματα: τα Λέλε και τα Μουμού. Κάθε Λέλε έχει 3 πόδια και κάθε Μουμού 7.  

Ο Πάικο, δηλαδή ο σπουδαίος διαστημικός εξερευνητής που ανακάλυψε τον πλανήτη Βουβού, είδε κάποτε ένα πλήθος από Λέλες και Μουμούς. Αν και το πλήθος ήταν γρήγορο και μπερδεμένο κατόρθωσε να διακρίνει ότι υπήρχε τουλάχιστον ένα άτομο από κάθε είδος, δηλαδή υπήρχε τουλάχιστον ένα Λέλε και ένα Μουμού. Ξαφνικά όλα τα πλάσματα του πλήθους ξάπλωσαν ανάσκελα και σήκωσαν τα πόδια τους στον αέρα. Ο Πάικο, παρά την τρομάρα του κατόρθωσε να μετρήσει τα πόδια τους. Ήταν 52 ακριβώς.
Πόσα Λέλες και πόσα Μουμούς μπορεί άραγε να ήταν εκεί;
Μπορείς να βρεις άλλες πιθανές απαντήσεις;

πηγή: https://nrich.maths.org/1005

πόσο ζυγίζει η πίτα;

H γιαγιά του Λευτέρη έφτιαξε πίτες για το σχολικό παζάρι. Φρόντισε να έχουν ακριβώς τα ίδια υλικά  και σε ίσες ποσότητες. Τώρα προσπαθεί να υπολογίσει το βάρος τους, αλλά έχει μόνο 2 βαρίδια για τη ζυγαριά της. Το ένα ζυγίζει 250 γραμμάρια και το άλλο 125. Η γιαγιά βρήκε ότι μια ολόκληρη πίτα ζυγίζει όσο τα δύο βαρίδια κι ένα τέταρτο της πίτας μαζί. Πόσο ζυγίζει η κάθε πίτα; 

πηγή: https://nrich.maths.org/1031 

Τέσσερις στη σειρά

Φτιάξτε μια αριθμογραμμή από το 0 ως το 20, όπως αυτή:

Μπορείτε να εκτυπώσετε μερικές με αυτή τη σελίδα.

Το παιχνίδι αυτό είναι για δύο παίκτες. Ο πρώτος διαλέγει δύο αριθμούς από το πλαίσιο που ακολουθεί και τους πολλαπλασιάζει ή τους διαιρεί. Στη συνέχεια διαγράφει από την αριθμογραμμή το αποτέλεσμα της πράξης.
Αν ο αριθμός είναι πολύ μικρός ή πολύ μεγάλος, ο παίκτης χάνει τη σειρά του.  

Ο δεύτερος παίκτης παίρνει σειρά και κάνει το ίδιο. Διαλέγει δηλαδή δύο αριθμούς από το πλαίσιο και τους πολλαπλασιάζει ή τους διαιρεί. Στη συνέχεια διαγράφει από την αριθμογραμμή το αποτέλεσμα της πράξης του με διαφορετικό χρώμα.

Νικητής είναι εκείνος που θα διαγράψει 4 αριθμούς στη σειρά. 

Με ποιο τρόπο μπορείς να κερδίσεις το παιχνίδι;

                                                                                         πηγή : http://nrich.maths.org/5633

μεγαλύτερο - μικρότερο 1

 

Ποιο είναι το μικρότερο αποτέλεσμα που μπορείς να βρεις αν κάνεις πράξεις με τους αριθμούς 3, 4, 5 και 6, χρησιμοποιώντας τον καθένα μόνο μία φορά; Ποιο είναι το μεγαλύτερο;

Μπορείς να κάνεις το ίδιο και με τους αριθμούς 1, 2, 3, 4, 5 και 6. 

πηγή: https://nrich.maths.org/primary-upper   

λαβύρινθος 100

Στον λαβύρινθο που ακολουθεί υπάρχουν αριθμοί, σημείο εκκίνησης (start) και σημείο τερματισμού (finish). Σε μια διαδρομή ξεκινάς από την εκκίνηση, τελειώνεις στο τέρμα και δεν μπορείς να περάσεις δύο φορές από τον ίδιο αριθμό. 
Μπορείς να επιλέξεις μια διαδρομή, έτσι ώστε προσθέτοντας τους αριθμούς από τους οποίους περνάς να αθροίσεις στο τέλος ακριβώς 100;  

Ποιο είναι το μικρότερο άθροισμα μιας πλήρους διαδρομής; 

Το μεγαλύτερο; (Θυμήσου ότι δεν μπορείς να περάσεις δυο φορές από τον ίδιο αριθμό.) 
                                                                 πηγή: https://nrich.maths.org/91