Σάββατο 19 Αυγούστου 2017
κλάσματα στην αριθμογραμμή
σε μορφή pdf εδώ .
πηγή: θέματα ε' τάξης από το διαγωνισμό της μαθηματικής εταιρείας
"Ο μικρός Ευκλείδης" (2017)
Παρασκευή 18 Αυγούστου 2017
Πέμπτη 17 Αυγούστου 2017
μαγικό ν
Βάλτε στους κύκλους του ν τος αριθμούς από το 1 ως το 5, με τέτοιο τρόπο ώστε τα αθροίσματα στις δύο γραμμές του ν να είναι ίσα.
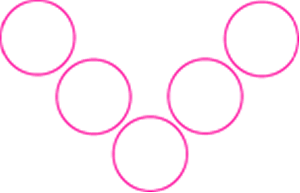
Πόσες διαφορετικές πιθανότητες υπάρχουν;
Τι κοινό έχουν όλες οι πιθανές λύσεις;
Μπορείτε να το εξηγήσετε;
Μπορείτε να πείσετε κάποιον ότι δεν υπάρχουν άλλες λύσεις;
Τι θα γινόταν αν χρησιμοποιούσαμε τους αριθμούς από το 12 ως το 16; Από το 27 ως το 41; Από το 103 ως το 107;Τι θα συνέβαινε σε ένα ν με 7 κύκλους, δηλαδή με 4 κύκλους σε κάθε γραμμή;
Να και μια αφίσα για το πρόβλημα
πηγή: https://nrich.maths.org/6274

Πόσες διαφορετικές πιθανότητες υπάρχουν;
Τι κοινό έχουν όλες οι πιθανές λύσεις;
Μπορείτε να το εξηγήσετε;
Μπορείτε να πείσετε κάποιον ότι δεν υπάρχουν άλλες λύσεις;
Τι θα γινόταν αν χρησιμοποιούσαμε τους αριθμούς από το 12 ως το 16; Από το 27 ως το 41; Από το 103 ως το 107;Τι θα συνέβαινε σε ένα ν με 7 κύκλους, δηλαδή με 4 κύκλους σε κάθε γραμμή;
Να και μια αφίσα για το πρόβλημα
πηγή: https://nrich.maths.org/6274
αγελάδες και πρόβατα
Στο λιβάδι της εικόνας που ακολουθεί μπορούμε να πούμε ότι κάθε αγελάδα μπορεί να δει 4 πρόβατα και 3 (άλλες) αγελάδες. Αυτό μπορεί κανείς να το εκφράσει ως εξής: "Κάθε αγελάδα βλέπει ένα πρόβατο περισσότερο απ' ό,τι αγελάδες". Όπως βλέπετε υπάρχουν 4 πρόβατα και 4 αγελάδες στο λιβάδι.
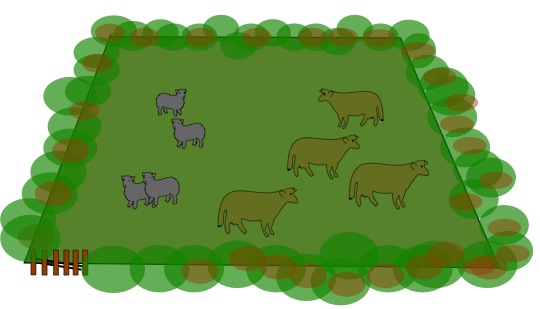
Ας δούμε όμως μερικά άλλα λιβάδια κι ας βρούμε πόσα πρόβατα και πόσες αγελάδες έχει το καθένα.
Στο πρώτο κάθε αγελάδα μπορεί να δει διπλάσια πρόβατα από αγελάδες και κάθε πρόβατο τον ίδιο αριθμό αγελάδων και προβάτων. Πόσα είναι τα πρόβατα και πόσες οι αγελάδες;
Στο δεύτερο, κάθε αγελάδα βλέπει τριπλάσια πρόβατα σε σχέση με τις αγελάδες και κάθε πρόβατο βλέπει ίσα αριθμό από τα δύο είδη ζώων.Πόσα είναι τα πρόβατα και πόσες οι αγελάδες;
Στο δεύτερο, κάθε αγελάδα βλέπει τριπλάσια πρόβατα σε σχέση με τις αγελάδες και κάθε πρόβατο βλέπει ίσα αριθμό από τα δύο είδη ζώων.Πόσα είναι τα πρόβατα και πόσες οι αγελάδες;
Στο τρίτο λιβάδι κάθε αγελάδα μπορεί να δει διπλάσια πρόβατα σε σχέση με τις αγελάδες και κάθε πρόβατο ένα πρόβατο παραπάνω από τις αγελάδες. Πόσα ζώα του κάθε είδους υπάρχουν στο τρίτο λιβάδι;
Στο τέταρτο λιβάδι κάθε αγελάδα μπορεί να δει διπλάσια πρόβατα από αγελάδες. Κάθε πρόβατο μπορεί να δει δύο περισσότερα πρόβατα από αγελάδες. Πόσες είναι οι αγελάδες και πόσα τα πρόβατα στο τέταρτο λιβάδι;
Στο πέμπτο λιβάδι, κάθε αγελάδα μπορεί να δει τριπλάσια πρόβατα από αγελάδες. Κάθε πρόβατο μπορεί να δει διπλάσια πρόβατα από αγελάδες. Πόσες είναι οι αγελάδες και πόσα τα πρόβατα;
Σάββατο 12 Αυγούστου 2017
Παρασκευή 11 Αυγούστου 2017
Πέμπτη 10 Αυγούστου 2017
Τρίτη 8 Αυγούστου 2017
ισοδύναμα κλάσματα
Για την κατανόηση της έννοιας εξαιρετικά χρήσιμες είναι οι
δραστηριότητες με τον τοίχο των κλασμάτων ή
η κατασκευή του από τους μαθητές.

Φυλλάδια για την εξάσκηση στα ισοδύναμα κλάσματα:
1. ισοδύναμα κλάσματα ακέραιας μονάδας με εικόνες
2. ισοδύναμα κλάσματα ακέραιας μονάδας με εικόνες
3. ισοδύναμα κλάσματα σε αριθμογραμμή
4. ασκήσεις απλοποίησης
5. συμπλήρωση όρου σε ισότητα κλασμάτων
6. συμπλήρωση κλάσματος σε σειρά ισοδύναμων .
δραστηριότητες με τον τοίχο των κλασμάτων ή
η κατασκευή του από τους μαθητές.

Φυλλάδια για την εξάσκηση στα ισοδύναμα κλάσματα:
1. ισοδύναμα κλάσματα ακέραιας μονάδας με εικόνες
2. ισοδύναμα κλάσματα ακέραιας μονάδας με εικόνες
3. ισοδύναμα κλάσματα σε αριθμογραμμή
4. ασκήσεις απλοποίησης
5. συμπλήρωση όρου σε ισότητα κλασμάτων
6. συμπλήρωση κλάσματος σε σειρά ισοδύναμων .
Δευτέρα 7 Αυγούστου 2017
εισαγωγή στα κλάσματα 2
1. Ένα βήμα στην πορεία κατανόησης της έννοιας του κλάσματος αποτελεί η επέκταση της εφαρμογής της από την ακέραιη μονάδα σε ένα πλήθος που δεν ταυτίζεται με τον παρονομαστή του κλάσματος, π.χ. τα 3/5 του 10. Εδώ και εδώ θα βρείτε εργασίες για το συγκεκριμένο θέμα.
 2. Μερικές φορές τα παιδιά δεν παρατηρούν ότι τα μέρη στα οποία χωρίζουμε μια ποσότητα ή μια μονάδα πρέπει να είναι ίσα μεταξύ τους για να σχηματιστούν κλάσματα. Εδώ υπάρχει ένα φυλλάδιο για την αντιμετώπιση του συγκεκριμένου θέματος.
2. Μερικές φορές τα παιδιά δεν παρατηρούν ότι τα μέρη στα οποία χωρίζουμε μια ποσότητα ή μια μονάδα πρέπει να είναι ίσα μεταξύ τους για να σχηματιστούν κλάσματα. Εδώ υπάρχει ένα φυλλάδιο για την αντιμετώπιση του συγκεκριμένου θέματος.
 2. Μερικές φορές τα παιδιά δεν παρατηρούν ότι τα μέρη στα οποία χωρίζουμε μια ποσότητα ή μια μονάδα πρέπει να είναι ίσα μεταξύ τους για να σχηματιστούν κλάσματα. Εδώ υπάρχει ένα φυλλάδιο για την αντιμετώπιση του συγκεκριμένου θέματος.
2. Μερικές φορές τα παιδιά δεν παρατηρούν ότι τα μέρη στα οποία χωρίζουμε μια ποσότητα ή μια μονάδα πρέπει να είναι ίσα μεταξύ τους για να σχηματιστούν κλάσματα. Εδώ υπάρχει ένα φυλλάδιο για την αντιμετώπιση του συγκεκριμένου θέματος.Κυριακή 6 Αυγούστου 2017
εισαγωγή στα κλάσματα
Στην ιστοσελίδα http://emathima.gr/ μπορείτε να βρείτε φυλλάδια για την εισαγωγή στα κλάσματα
Πιο συγκεκριμένα, από εκεί μπορείτε να κατεβάσετε υπάρχουν 4 φυλλάδια για:
Σκιάσεις μερών και ονομασία σκιασμένων μερών

ονομασία σκιασμένων μερών και μισά
σκιάσεις μερών και αντιστοιχίσεις σκιασμένων μερών με κλάσματα
σκιάσεις μερών και επιλογή σωστού κλάσματος για σκιασμένο μέρος.
Επίσης στην ίδια ιστοσελίδα μπορείτε να βρείτε
πολύ απλές καρτέλες κλασμάτων και
λιγότερο απλές καρτέλες κλασματικών μονάδων, όπου εμφανίζονται και οι αντίστοιχοι δεκαδικοί αριθμοί και τα αντίστοιχα ποσοστά στα εκατό.
ακολουθίες Φάρεϋ
Είναι εύκολο να τοποθετήσουμε στη σειρά, από το μικρότερο προς το μεγαλύτερο, μια σειρά δεκαδικών αριθμών. Αλλά τι γίνεται με τα κλάσματα;
Κάποτε, ένας κύριος που λεγόταν John Farey ανακάλυψε σειρές κλασμάτων κατά μέγεθος (από το μικρότερο προς το μεγαλύτερο), τις ονόμασαν ακολουθίες Φάρεϋ.
Η τρίτη ακολουθία Φάρεϋ είναι έτσι:
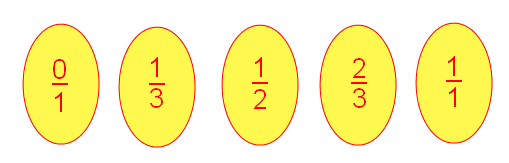
Περιέχει σε σειρά μεγέθους όλα τα κλάσματα μεταξύ του 0 και του 1, στην απλούστερη μορφή τους και με παρονομαστές που δεν ξεπερνούν το 3.
Συνεχίζουμε με την τέταρτη ακολουθία Φάρεϋ.

Μπορείτε να βρείτε την πέμπτη;
Ποια επιπλέον κλάσματα εμφανίζονται στην πέμπτη ακολουθία, ενώ δεν υπήρχαν στην τέταρτη;
Χρησιμοποιήστε την πέμπτη ακολουθία για να φτιάξετε την έκτη και την έβδομη.
Να και κάποια επιπλέον ερωτήματα:
Στην ενδέκατη ακολουθία υπάρχουν πολλά κλάσματα που δεν υπήρχαν στην δέκατη.
Υπάρχουν όμως μονάχα λίγα κλάσματα που εμφανίζονται στην δωδέκατη ακολουθία και δεν υπάρχουν στην ενδέκατη.
Μπορείτε να εξηγήσετε γιατί;
Πότε χρειαζόμαστε πολλά καινούργια κλάσματα για την επόμενη ακολουθία Φάρεϋ;
Κάθε Ακολουθία Φάρεϋ είναι μεγαλύτερη από την προηγούμενη; Πώς το ξέρουμε;
Μέχρι τώρα κάθε ακολουθία Φάρεϋ περιέχει ένα μονό αριθμό κλασμάτων. Μπορείς να βρεις μια ακολουθία Φάρεϋ με ζυγό αριθμό κλασμάτων;
σκάλες
Με ένα τουβλάκι φτιάχνω μια πολύ απλή σκάλα: ένα βήμα ανόδου κι ένα βήμα καθόδου.
Με τέσσερα τουβλάκια φτιάχνουμε μια σκάλα με δύο βήματα ανόδου και δύο βήματα καθόδου
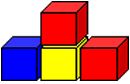
Πόσα τουβλάκια θα χρειαστούμε για να φτιάξουμε μια σκάλα με πέντε βήματα ανόδου και πέντε βήματα καθόδου;
Μπορείτε να εξηγήσετε πως θα βρίσκουμε το πλήθος από τουβλάκια που θα χρειαστούμε για να φτιάξουμε σκάλες κάθε μεγέθους;
γαλάζιο και μπλε
Ψάχνουμε το μέρος (κλάσμα) που καταλαμβάνει το γαλάζιο σε κάθε τετράγωνο.

Μπορείς να βρεις ποια θα ήταν τα δύο επόμενα τετράγωνα, αν συνεχίζαμε με τον ίδιο τρόπο;
πηγή: https://nrich.maths.org/2105
το μουσείο των κλασμάτων
Στο βίντεο που ακολουθεί, ο δάσκαλος αξιοποιεί την ιδέα του μουσείου και των εκθεμάτων του, για να ωθήσει τα παιδιά να εμβαθύνουν στην έννοια του κλάσματος. Τα παιδιά "κατασκευάζουν" κλάσματα, τα εκθέτουν, συζητούν γι' αυτά με τους συμμαθητές τους, τα εξηγούν, φτιάχνουν μικρά αινίγματα και παίζουν μ' αυτά.
Δυστυχώς, δεν υπάρχει μετάφραση.
https://www.youtube.com/watch?v=lizNJthlpr8
Σάββατο 5 Αυγούστου 2017
τρίγωνο
Παρακολουθήστε το βίντεο BryonyTriangle.mp4 στο οποίο η παρουσιάστρια δείχνει πως να φτιάξουμε ένα λουλούδι από ένα τετράγωνο χαρτί.
Στη συνέχεια θέτει ένα προκλητικό ερώτημα: τι μέρος (κλάσμα) του τετράγωνου χαρτιού αποτελεί το σκιασμένο τρίγωνο;
πηγή: https://nrich.maths.org/7392
κόβουμε στη μέση
Μπορείτε να κόψετε κάθε ένα από τα παρακάτω σχήματα έτσι ώστε τα δύο κομμάτια του να είναι ακριβώς ίδια μεταξύ τους;
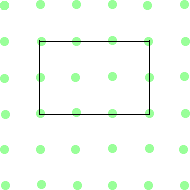 |  |
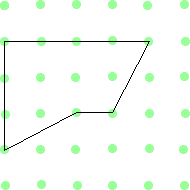 | 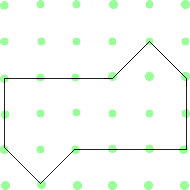 |
φυλλάδιο: εδώ
τετράγωνο, τρίγωνα, κλάσματα
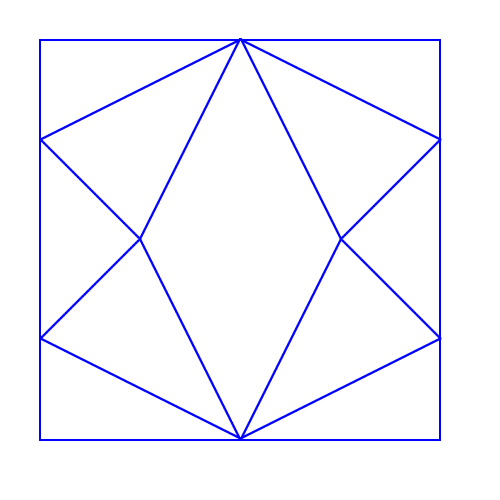
Στο σχέδιο που ακολουθεί έχουμε ένα τετράγωνο. Από την πάνω δεξιά γωνία του χαράξαμε δύο ευθείες προς το μέσο των απέναντι πλευρών. Στη συνέχεια με μία νέα ευθεία ενώσαμε τα δύο μέσα.
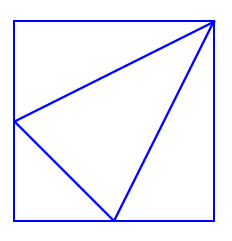
Τι μέρος (κλάσμα) της επιφάνειας του τετραγώνου αποτελεί κάθε τρίγωνο;
Στη συνέχεια, χρησιμοποιώντας το πρώτο σχέδιο, σχεδιάσαμε την εικόνα που ακολουθεί. Πώς;
Ποιο γεωμετρικό σχήμα εμφανίζεται στο κέντρο του σχεδίου μας;
Τι μέρος (κλάσμα) του συνολικού σχεδίου αποτελεί;
στα 2;
Κάποιος προσπάθησε να κόψει τα παραλληλόγραμμα σε δύο ίσα μέρη. Τα κατάφερε; πώς μπορείς να το ελέγξεις;


πηγή: https://nrich.maths.org/1788
πρόσθετα υλικά: 1 , 2
εφαρμογή για κλάσματα
Ο σύνδεσμος που ακολουθεί παραπέμπει σε μία ηλεκτρονική εφαρμογή που μπορεί να φανεί χρήσιμη σε δασκάλες και δασκάλους που διαθέτουν διαδραστικό πίνακα (ή υπολογιστή και προτζέκτορα) και σύνδεση με το διαδίκτυο στην τάξη τους.
Κάνει λίγο πιο εύκολη τη διδασκαλία της έννοιας του κλάσματος και τις συγκρίσεις κλασμάτων.
Κερδίζεις χρόνο κι έτσι διευκολύνεις την μετατροπή των εννοιών σε εικόνες. Ίσως όμως χάνεις σε σκέψη και φαντασία. Θα ήταν προτιμότερο να χρησιμοποιείται με μέτρο.
https://www.mathlearningcenter.org/web-apps/fractions/
Κάνει λίγο πιο εύκολη τη διδασκαλία της έννοιας του κλάσματος και τις συγκρίσεις κλασμάτων.
Κερδίζεις χρόνο κι έτσι διευκολύνεις την μετατροπή των εννοιών σε εικόνες. Ίσως όμως χάνεις σε σκέψη και φαντασία. Θα ήταν προτιμότερο να χρησιμοποιείται με μέτρο.
https://www.mathlearningcenter.org/web-apps/fractions/
μοιράζοντας στα 2
Μπορείς να κόψεις ένα χαρτί Α4 σε δύο ίσα μέρη; Μπορείς να το κάνεις με πολλούς τρόπους; Με πόσους;
Προσπάθησε να βρεις όσους περισσότερους μπορείς. Μην το φοβάσαι, δοκίμασε διάφορους.
Μπορείς να ξεκινήσεις μ' αυτούς τους δύο.


Πώς θα βεβαιώνεσαι κάθε φορά ότι τα κομμάτια που έκοψες είναι ίσα;
Μπορείς να ξεκινήσεις μ' αυτούς τους δύο.


Πώς θα βεβαιώνεσαι κάθε φορά ότι τα κομμάτια που έκοψες είναι ίσα;
ένα μπολ με φρούτα
Στην εικόνα που ακολουθεί βλέπουμε μια φρουτιέρα.

Τα μισά από τα φρούτα της είναι μήλα. Υπάρχουν επίσης 3 πορτοκάλια, 2 αχλάδια και μία μπανάνα.
Πόσα είναι τα μήλα;
Αν το ένα τέταρτο ήταν μήλα και το άλλο ένα τέταρτο πορτοκάλια και υπήρχαν επίσης 4 μπανάνες, 3 αχλάδια και 3 μανταρίνια, πόσα θα ήταν τα μήλα; Πόσα φρούτα θα είχε η φρουτιέρα;
Πόσα είναι τα μήλα;
Αν το ένα τέταρτο ήταν μήλα και το άλλο ένα τέταρτο πορτοκάλια και υπήρχαν επίσης 4 μπανάνες, 3 αχλάδια και 3 μανταρίνια, πόσα θα ήταν τα μήλα; Πόσα φρούτα θα είχε η φρουτιέρα;
για τα μισά και τα ολόκληρα
Σύγκρινε τα αντικείμενα μεταξύ τους. Στο ίδιο χρώμα και ανάμεσα στα χρώματα. Τι παρατηρείς;
Μπορείς να εξηγήσεις πως σκέφτηκες;

Είναι όλα τα ολόκληρα ίδια; Είναι όλα τα μισά ίδια; Τι συμπέρασμα βγάζεις για το 1 και για το 1/2;
κατασκευάζοντας τον τοίχο των κλασμάτων
Στο βίντεο αυτό, παρουσιάζεται μια ιδέα για την εισαγωγή στην έννοια του κλάσματος ή του ισοδύναμου κλάσματος.
Με ψαλίδι, χαρτόνι και μαρκαδόρους τα παιδιά κατασκευάζουν τον τοίχο των κλασμάτων.
Από εκεί και πέρα οι δραστηριότητες που μπορούν να γίνουν μ' αυτόν είναι πολλές.
Δεν είναι ανάγκη να παρακολουθήσει κανείς και τα 9 λεπτά του βίντεο. Αρκεί να δει από το 2:00 ως το 6:30 περίπου.
https://www.youtube.com/watch?v=PmWnMtLBJZM
Δευτέρα 31 Ιουλίου 2017
ο τοίχος των κλασμάτων 2
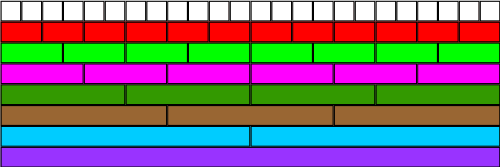
Ποιο είναι μεγαλύτερο το ένα τρίτο ή τα δύο όγδοα; Πόση είναι η διαφορά τους; Αξιοποιήστε την εικόνα του τοίχου των κλασμάτων για να βεβαιωθείτε ότι απαντήσατε σωστά.
Ποιο είναι μικρότερο τα πέντε έκτα ή τρία τέταρτα; Πόση είναι η διαφορά τους;
Ποια είναι διαφορά ανάμεσα στα πέντε έκτα και το ένα τρίτο;
Ποια είναι τα τρία τέταρτα του δύο τρίτα; Μπορείς να εξηγήσεις πως το βρήκες;
Σοκολάτα
Στη δραστηριότητα αυτή ασχολούμαστε με σοκολάτες. Φανταστείτε ότι όσοι συμμετέχουν σ' αυτή θέλουν να πάρουν όσο το δυνατόν περισσότερη.
Σε μια αίθουσα του σχολείου έχουμε τρία τραπέζια και άφθονο χώρο γύρω τους για να βάλουμε όσες σοκολάτες θέλουμε. Στο πρώτο τραπέζι έχουμε μια πλάκα σοκολάτας, στο δεύτερο τραπέζι δύο μπάρες και στο τρίτο 3.
Έξω από την αίθουσα υπάρχει μια μεγάλη ουρά μαθητών που περιμένουν να πάρουν τις σοκολάτες. Ο κανόνας λέει ότι κάθε παιδί μπαίνει στην αίθουσα, μονάχα αφού ο μπροστινός του έχει ήδη κάτσει. Μετά διαλέγει τραπέζι και από την στιγμή που θα κάτσει δικαιούται το μερίδιο που του αναλογεί από το τραπέζι. Έτσι όποτε κάποιος μπαίνει στην αίθουσα πρέπει να αναλογιστεί: "Αν η σοκολάτα του τραπεζιού που θα διαλέξω μοιραστεί δίκαια, σε ποιο τραπέζι με συμφέρει να κάτσω;" Κανείς δεν ξέρει σε ποιο σημείο θα απαγορευτεί η είσοδος κι άλλων μαθητών.
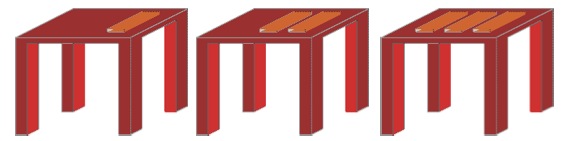
Ωστόσο, η πράξη της μοιρασιάς δεν αρχίζει μέχρις ότου κάτσουν όλα τα παιδιά.
"αν πάω στο πρώτο τραπέζι θα γίνουμε τρεις, θα πάρω δηλαδή το 1/3,
αν πάω στο δεύτερο θα γίνουμε 4, θα πάρω δηλαδή τα 2/4,
αν πάω στο τρίτο τραπέζι θα γίνουμε 4, θα πάρω δηλαδή τα 3/4. Τα 3/4 είναι η καλύτερη (μεγαλύτερη) από τις επιλογές μου, άρα θα πάω στο τρίτο τραπέζι."
Στη συνέχεια συζητήστε με συμμαθητές σας και συγκρίνετε την πορεία που σκεφτήκατε με τη δική τους. Διαλέξτε ποια διαδρομή ήταν η καλύτερη κατά τη γνώμη σας και εξηγήστε το γιατί.
Σε μια αίθουσα του σχολείου έχουμε τρία τραπέζια και άφθονο χώρο γύρω τους για να βάλουμε όσες σοκολάτες θέλουμε. Στο πρώτο τραπέζι έχουμε μια πλάκα σοκολάτας, στο δεύτερο τραπέζι δύο μπάρες και στο τρίτο 3.
Έξω από την αίθουσα υπάρχει μια μεγάλη ουρά μαθητών που περιμένουν να πάρουν τις σοκολάτες. Ο κανόνας λέει ότι κάθε παιδί μπαίνει στην αίθουσα, μονάχα αφού ο μπροστινός του έχει ήδη κάτσει. Μετά διαλέγει τραπέζι και από την στιγμή που θα κάτσει δικαιούται το μερίδιο που του αναλογεί από το τραπέζι. Έτσι όποτε κάποιος μπαίνει στην αίθουσα πρέπει να αναλογιστεί: "Αν η σοκολάτα του τραπεζιού που θα διαλέξω μοιραστεί δίκαια, σε ποιο τραπέζι με συμφέρει να κάτσω;" Κανείς δεν ξέρει σε ποιο σημείο θα απαγορευτεί η είσοδος κι άλλων μαθητών.

Ωστόσο, η πράξη της μοιρασιάς δεν αρχίζει μέχρις ότου κάτσουν όλα τα παιδιά.
Είναι μάλλον εύκολο να διαλέξει κανείς τραπέζι αν είναι στην αρχή. Όσο όμως προχωρά η διαδικασία γίνεται όλο και δυσκολότερο.
Ας πούμε ότι έχουν ήδη μπει 8 παιδιά. Τώρα είναι η σειρά σας. Μπαίνετε στο δωμάτιο και βλέπετε
Ας πούμε ότι έχουν ήδη μπει 8 παιδιά. Τώρα είναι η σειρά σας. Μπαίνετε στο δωμάτιο και βλέπετε
2 παιδιά στο πρώτο τραπέζι3 παιδιά στο δεύτερο τραπέζι3 παιδιά στο τρίτο τραπέζι
Πώς θα διαλέξετε τραπέζι;
Εγώ στη θέση σας θα σκεφτόμουν
Εγώ στη θέση σας θα σκεφτόμουν
"αν πάω στο πρώτο τραπέζι θα γίνουμε τρεις, θα πάρω δηλαδή το 1/3,
αν πάω στο δεύτερο θα γίνουμε 4, θα πάρω δηλαδή τα 2/4,
αν πάω στο τρίτο τραπέζι θα γίνουμε 4, θα πάρω δηλαδή τα 3/4. Τα 3/4 είναι η καλύτερη (μεγαλύτερη) από τις επιλογές μου, άρα θα πάω στο τρίτο τραπέζι."
Στη συνέχεια συζητήστε με συμμαθητές σας και συγκρίνετε την πορεία που σκεφτήκατε με τη δική τους. Διαλέξτε ποια διαδρομή ήταν η καλύτερη κατά τη γνώμη σας και εξηγήστε το γιατί.
ο τοίχος των κλασμάτων
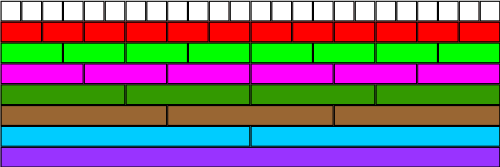
Χρησιμοποιώντας την παραπάνω εικόνα, βρείτε όλους τους δυνατούς τρόπους για να γράψατε με κλάσμα το μισό.
Με τη βοήθεια της εικόνας, μπορείτε να βρείτε ισοδύναμα του 13 ; πόσα;
Χρησιμοποιώντας και πάλι την εικόνα του τοίχου των κλασμάτων, γράψτε με διαφορετικούς τρόπους τα 34;
Μήπως μπορείτε να βρείτε κάποιον κανόνα για να δουλεύετε με τα ισοδύναμα κλάσματα;
Κλάσματα μήκους
Στο παρακάτω σχέδιο μπορείτε να δείτε 7 μπάρες διαφορετικού χρώματος. Κάθε μία φτιάχνεται από διαφορετικό πλήθος τετράγωνων, το οποίο είναι γραμμένο στο τέλος της.
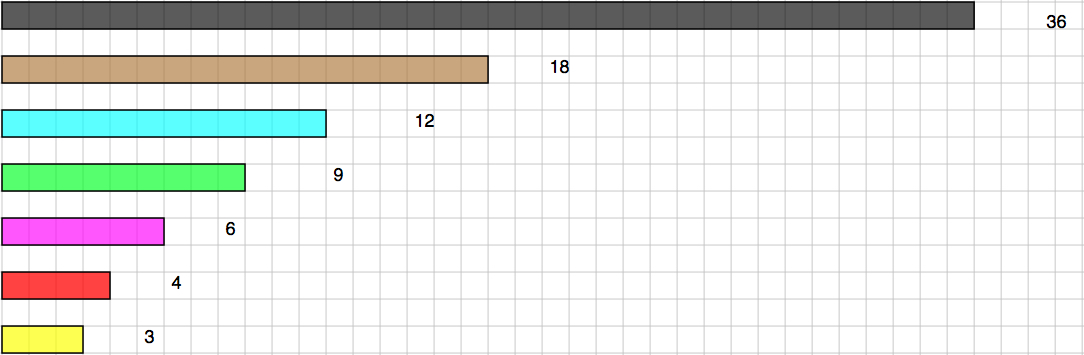
Για να ξεκινήσετε υπολογίστε τη μαύρη μπάρα ως 1, άρα η καφέ είναι το
Χρησιμοποιώντας διαφορετικούς συνδυασμούς, προσπαθήστε να φτάσετε στο μήκος της μαύρης μπάρας, δηλαδή στο 36.
Στη συνέχεια γράψτε τη λύση σας με δύο τρόπους.
Για παράδειγμα αν βάλετε την καφέ μπάρα μαζί με τη γαλάζια και την ροζ θα τα έχετε καταφέρει και πρέπει να γράψετε:
α.
18 + 12 + 6 = 36
και β.
- - - - - - - - - - - - - - - - - -
Συνέχεια 1
Διαλέξτε 4 μπάρες (εκτός από τη μαύρη) και συγκρίνετε το άθροισμα τους με τη μαύρη μπάρα.
Ακολουθούν δύο παραδείγματα:
1.

Αθροίζοντας το κίτρινο (3), το ροζ (6), το γαλάζιο (12) και το καφέ (18),
φτάνουμε 39, δηλαδή στο 1 ολόκληρο και ένα δωδέκατο.
2. Χρησιμοποιώντας 2 γαλάζια (2Χ12) και δύο πράσινα (2Χ9) φτάνουμε στο 42, δηλαδή στο 1 ολόκληρο και ένα έκτο.
1
- - - - - - - - - - - - - - - - - -
Συνέχεια 2
Τώρα η γαλάζια μπάρα θα είναι το 1. Χρησιμοποιήστε τις τετράδες που έχετε ήδη φτιάξει, και συγκρίνετε τις με τη γαλάζια, αντί για τη μαύρη μπάρα.
Στο πρώτο από τα παραδείγματα μας (κίτρινο + ροζ + γαλάζιο + καφέ) η σύγκριση θα μας έβγαζε τρεις ολόκληρες γαλάζιες μπάρες και ένα τέταρτο της.

Στο δεύτερο παράδειγμα ( γαλάζια + γαλάζια + πράσινη + πράσινη) η σύγκριση θα μας έβγαζε 3 γαλάζιες και μισή ακόμη.

Τώρα κάνετε τις δικές σας συγκρίσεις.
- - - - - - - - - - - - - - - - - -
Πως θα σχολιάζατε τα αποτελέσματα των συγκρίσεων πρώτα με τη μαύρη μπάρα και μετά με την γαλάζια;
πηγή: https://nrich.maths.org/12935
πηγή: https://nrich.maths.org/12935
Εγγραφή σε:
Σχόλια (Atom)














